Intro

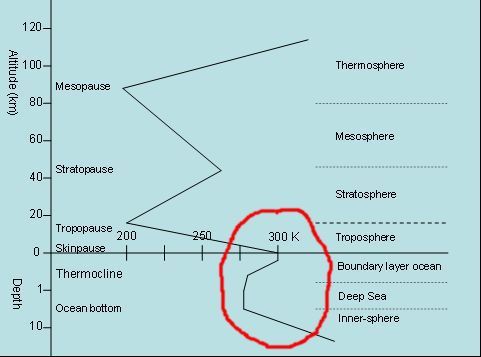
Een transparant medium gedraagt zich in een stralingsveld anders dan een ondoorzichtig. Dat is voor het klimaat belangrijk. 70% van het aardoppervlak is oceaan. Dat is net als de atmosfeer een transparant medium, dus reden om transparantie nader te bezien. De warmte inhoud van de oceaan is beduidend groter dan van de atmosfeer.
Talloze verhandelingen over klimaat gaan impliciet uit van een ondoorzichtige aarde. Of dat terecht is, zou moeten blijken. In beide voorgaande artikelen in deze serie en hier staat aanleiding tot twijfel.
Eerder al bleek een andere belangrijke aanname in genoemde verhandelingen ondeugdelijk. De atmosferische broeikas zou de 30 °C verschil overbruggen tussen de gemeten temperatuur en die van een atmosfeervrije aarde. Dat is onjuist. Het verschil is groter. Dus indien de broeikas het bewerkstelligt, moet hij sterker zijn dan men aanneemt. Dan is hij niet goed uitgerekend. Waren die berekeningen wel goed, dan is er een ander mechanisme dat helpt de aarde leefbaar te houden. Roy W. Spencer, een bekend klimatoloog, gaf aan dat de 30 °C - hij schrijft 33 °C, het verschil is hier niet van belang - eenvoudig het verschil is tussen het veronderstelde stralingsevenwicht en de gemeten temperatuur. Hij bekritiseert de te lage schatting van het te overbruggen verschil. Volgens hem is dat verschil ~60 °C. Maar zijn verklaring voor de lagere evenwichtemperatuur is anders dan die van de onvolledige temperatuur-verevening.
Meer hierover in Noot (1).


Een transparante staaf

In een gedachten experiment onderzoeken we een geïsoleerde transparante staaf loodrecht op de kop bestraald door een evenwijdige bundel. De absorptie coëfficiënt k is gelijk voor alle golflengten van de bundel. In stationaire toestand blijft de temperatuur op elke dwarsdoorsnede onveranderd. De daar ontvangen energie moet in zijn geheel worden afgevoerd. Aannemend dat het medium ondoorzichtig is voor langgolvig (rood) licht - we houden de oceaan in gedachten - kan dat alleen door materiestroming en geleiding. Geleiding wordt beschreven met coëfficiënt λ. We doen of het transport door stroming net zo kan worden beschreven en gebruiken de energietransport coëfficiënt λ'. De uitgaande energie flux is gelijk aan de binnenkomende, I_o. Dat gaat door geleiding, oppervlaktestraling en eventueel verdamping. De verdeling tussen de drie komt er niet op aan indien we alleen geïnteresseerd zijn in het temperatuur verloop in langsrichting ΔT_x, waarin x de afstand tot het kopvlak is. De referentie temperatuur T_o mag elke waarde hebben. We veronderstellen de parameters temperatuuronafhankelijk. Denk aan de infinitesimale laag onder die waar de uitwisseling met de omgeving plaatsvindt.

Parameters en algoritmen:

• I_x = I_o.e^-kx Wm^-2 (absorptie wet), waarin I_o de straling influx is en I_x wat er na x m van over is.
• k (absorptiecoëfficiënt) = 9,21034.10-3 m^-1. Zo gekozen dat I₁₀₀₀ / I_o = 10^-4. (Denk aan de oceaan, 1000 m diep nog een verwaarloosbaar 1/10000^ste van de straling over.)
• Een laag op op x m absorbeert I_x.kdx Wm^-2.
• λ'.dT/dx Wm^-2 (warmtetransport door temperatuurgradiënt).
• λ' = 12 W.m^-1.K^-1. De geleidingscoëfficiënt van water is 0,6; die van koper 390. In vloeistof gaat het transport in hoofdzaak door stroming. We doen een gis, maar λ' zou ook 500 kunnen zijn (!).
• I_o = 1000 Wm^-2 ongeveer de maximale zon instraling na aftrek van een gemiddeld albedo.

Alle straling die laag x passeert belandt in stationaire toestand op de terugweg in laag x als warmte, die het door geleiding/stroming doorgeeft aan de volgende laag. Daarbij vergeleken is de in de laag geabsorbeerde stralingsenergie verwaarloosbaar. De berekening van ΔT_x

Intro

In a radiation field a transparent medium behaves unlike an opaque. That is important for the earth's climate. 70% of the earth's surface is ocean. Just like the atmosphere, this is a transparent medium. So transparency is worth considering. In addition the heat content of the ocean is significantly greater than that of the atmosphere.
Countless treatises on climate implicitly assume an opaque earth. Whether that is justified thus needs consideration. In both previous articles in this series and here that assumption seemed to be doubtful.
Earlier, another important assumption in the aforementioned treatises proved inadequate. The atmospheric greenhouse would bridge the 30 °C difference between the measured temperature and that of an atmosphere-free earth. That is incorrect. The difference is greater. So if the greenhouse produces it, it must be stronger than one assumes. Then it cannot be calculated correctly. If these calculations were correct, then there is another mechanism that helps to keep the earth livable. Roy W. Spencer, a renowned climatologist, indicated that the 30 °C - he writes 33 °C, the difference is irrelevant here - is simply the difference between the supposed radiation equilibrium and the measured temperature. He criticizes the too low estimate of the gap. According to him it should be 60 °C. However he suggests a lower equilibrium for a different reason than non-uniformity of the surface temperature.
More about this in Note (1).


A transparent bar

In a thought experiment we examine an isolated transparent bar irradiated by a parallel beam perpendicular to the head. The absorption coefficient k is assumed to be equal for all wavelengths of the beam. In the stationary state the temperature remains unchanged at every cross-section. The energy received there must be discharged in its entirety. Assuming that the medium is opaque to long-wave (red) light - we keep the ocean in mind - this is only possible through material flow and conduction. Conduction is described with coefficient λ. We do, as if the transport can be described by flow in the same way, and use the 'energy transport coefficient' λ'. The outgoing energy flux is equal to the incoming, I_o. It is made up of conduction, surface radiation and possibly evaporation. The division between the three is not important if we are only interested in the temperature gradient in the longitudinal direction ΔT_x, where x is the distance to head surface. The reference temperature T_o may have any value. We assume the parameters are temperature independent. Think of the infinitesimal layer just below the head surface, where the exchange with the environment takes place.

Parameters and algorithms;

• I_x = I_o.e^-kx Wm^-2 (absorption law), where I_o is the radiation influx and I_x what is left after x m.
• k (absorption coefficient) = 9.21034.10^-3m^-1. So chosen that I₁₀₀₀ / I_o = 10^-4. (Think about the ocean, 1000 m deep, a negligible 1/10000^th left of the radiation.)
• A layer at x m absorbs I_x.kdx Wm^-2
• λ'.dT/dx Wm^-2 (heat transport by temperature gradient).
• λ' = 12 W.m^-1.K^-1. The conduction coefficient of water is 0,6; that of copper 390. In liquid, the transport mainly goes through mass flow. We are doing a guess, but λ' could also be 500 (!).
• I_o = 1000 Wm^-2, about the maximum sun irradiation after the deduction of an average albedo.

In stationary state all radiation passing through layer x ends up as heat on the way back in layer x. Here it passes on through conduction/convection to the next layer. In comparison, the incoming radiation energy absorbed in the layer is negligible. The calculation of ΔT_x

With the indicated parameters this provides the temperature profile in table 1.

Een transparant medium in evenwicht met inkomende straling kan inwendig verrassend hoge temperaturen te zien geven. Het tabel profiel lijkt niet op het gemeten profiel, de thermocline, in de oceaan. Dat is niet verbazingwekkend omdat het model totaal verschilt van de oceanische realiteit(2). Merk verder op dat bij grote diepte in het staafmodel de energietransporten zo gering zijn, dat een hittebestendig, langszwemmend visje of een zinkende alg het profiel in de war gooit. Op 1000 m levert de straling nog I_x.k = 0,0009 Wm^-3. (De relaxatietijd voor het instellen van evenwicht is dus lang; ~1500 jaar om een kubieke meter 1 °C op te warmen.)
De conclusie van dit gedachten experiment is:

Straling veroorzaakt binnen een zwak absorberend medium hogere temperaturen dan aan het oppervlak volgens Stefan-Boltzman.

Dit is van belang voor klimaatbeschouwingen. Zowel de atmosfeer als de oceaan zijn transparant. Daarbij is de warmte inhoud van het deel van de oceaan dat bij het klimaat is betrokken veel groter dan dat van de lucht. Misschien is de broeikas zelfs niet of beperkt nodig?

Meer inzicht in het gedrag van transparante media zou verhelderend zijn voor bepaalde klimatologische vraagstukken. Bv. Modelberekening aan

• Een gedeelde staaf met verschillende k en λ' (denk aan lucht en water).
• Een roterende staaf (imitatie van dag en nacht).
• Het medium niet opake voor infra rood. Een transparant lichaam straalt niet vanaf het oppervlak, maar ook van binnen uit.
• Variatie in de verdeling van de uitgaande energie door geleiding, verdamping en straling. Zie Hughes voor de invloed op de temperatuur.
• Een bol in de plaats van een staaf?

Noten

1. Met dank aan Hans W. Erren en C.A. (Kees) de Lange. De laatste wees op publikaties van
∘ Murry L. Salby "Fundamentals of atmospheric physics" (Acad.Press 1995)
∘ en een 'Twitter' van Ed Nikolov. waarin hij een aardse stralings evenwichttemperatuur van 197 K noemt.
∘ Erren tipte de boven al aangehaalde webpagina van Roy Spencer. Die net als Salby en
∘ Egbert Boeker en Van Grondelle in "Environmental Physics" (Wiley 1999) de grootte van het broeikas effect aanduiden als verschil tussen gemeten temperatuur en berekend uit het stralingsevenwicht.
Boeker expliciteert dat het verschil met 255 K van atmosferische oorsprong is, CO₂, O₃. N₂O & CH₄ i.h.b.. Spencer suggereert een 60 °C kloof gecompenseerd door 'stroming', terwijl Nikolev's twitter de hogere meettemperatuur toeschrijft aan adiabatische compressie.
Het effect van de slechts gedeeltelijke temperatuurverevening op aarde en de wiskundige eigenschap <T⁴>≠<T>⁴ lijkt in klimaatstudies niet erg bekend.

2. Convectie kan effectiever warmte transporteren dan geleiding. Indien we λ' = 500 hadden gekozen, zouden alle ΔT_x in tabel 1 ~40x lager zijn uitgekomen.

3. Ad Huijser corrigeerde de formule voor ΔT_x door mijn opmerking over de irrelevantie van de waarde van T_o in de formule op te nemen. Voor de uitkomsten in de tabel maakt het geen verschil.

A transparent medium in balance with incoming radiation can show surprisingly high temperatures internally. The table profile does not resemble the measured profile, the thermocline, in the ocean. That is not surprising because the model is completely different from the oceanic reality(2). Note furthermore that at large depths in the bar model the energy transports are so small that a heat-proof, swimming fish or sinking algae destroys the profile. At 1000 m the radiation yields I_x.k = 0.0009 Wm^-3 only. (The relaxation time for setting a balance is therefore long: ~ 1500 years to heat up a cubic meter 1 °C.).
The conclusion of this thought experiment is:

Radiation causes higher temperatures within a weakly absorbing medium than it does on the surface according to Stefan-Boltzman.

This is important for climate considerations. Both the atmosphere and the ocean are transparent. In addition, the heat content of the part of the ocean, that is involved in the climate, is much greater than that of the air. Perhaps the greenhouse is not even needed or or only partly?

More insight into the behavior of transparent media would be illuminating certain climatic issues. We therefor need model calculations e.g.

• A divided bar with different k and λ' (think of air and water).
• A rotating bar (imitation of day and night).
• A bar of material that is not opaque for infra red. A transparent body does not radiate from the surface alone, but also from the inside out.
• Variation in the distribution of the outgoing energy between conduction, evaporation and radiation. See Hughes for the influence on temperature.
• A sphere instead of a bar?

Notes

1. With thanks to Hans W. Erren and C.A. (Kees) de Lange. The latter pointed to publications by
∘ Murry L. Salby "Fundamentals of atmospheric physics" (Acad.Press 1995),
∘ and a 'Twitter' by Ed Nikolov. Nikolev mentions a terrestrial radiation equilibrium temperature of 197 K.
∘ Erren drew attention to the webpage of Roy Spencer, mentioned already in the text, who like Salby and
∘ Egbert Boeker and Van Grondelle in "Environmental Physics" (Wiley 1999) treat the greenhouse effect as bridging the gap between measured temperature and the calculated radiation equilibrium.
Boeker states explicitly that the difference from 255 K is of atmospheric origine, CO₂, O₃, N₂O & CH₄ in particular. Spencer suggests a 60 °C lower calculated temperature, due to 'flow', while Nikolev's twitter attributes heating to the adiabatic lapse rate.
The effect of the only partial temperature equalization on earth and the mathematical property <T⁴>≠<T>⁴ is not very well known in climate studies.

2. Convection is able to transport heat more effective than conduction. If we would have chosen λ' = 500, all ΔT_x in table 1 would have been ~40x lower.

3. Ad Huijser corrected the formula for ΔT_x by including my remark about the irrelevance of the value of T_o and insert it in the formula. The correction does not change the results listed in the table.

This article is published also on Principia Scientific International