

A watery planet
In a previous article1,"Climate, radiation and temperature equalization-2" (in Dutch), I treated the radiation balance of an opaque black body at the same distance from the sun as the earth.
Equilibrium temperatures locally as well as the average one were found to strongly depend on the way in which the body distributes the incoming solar energy. I.e. the heat transport along the surface (and the effects of its rotation, if it were the earth) under the same sun.
70% of the earth's surface is ocean. It is not opaque. The sunlight penetrates to a depth of more than
100 metres. The question arises, how this affects the temperature distribution and the radiation balance?
If a parallel light beam with energy flux Io (W/m2) hits a transparent medium, it is absorbed gradually. At a depth x the remaining flux is:
(Each layer dx absorbs Ix.kdx.) This formula applies only to radiation of a certain frequency. Materials have frequency-dependent absorption coefficients k. For water the k for blue light is much smaller than for infrared (IR). The penetration depth of IR is only a few mm while that for blue light is in the order of 100+ m.
For a rotating body, such as the earth, Io is place and time dependent. At a clear night it is low.
The consequences of this for the radiation balance and to a certain extent the temperature were treated by Geraint Hughes2 in
"The Watery Planet" on 21 August 2018.
He calculates a reduction of the effective emissivity ε of the earth to 0,6, which would bring the average temperature to 288 K, due to heat transport by evaporation. This result corresponds fairly accurately with the value calculated in my aforementioned article1, Table 3 (bare sphere with ideal temperature equalization at ε = 0,6 and α = 0,3).
In his article, "Evaporation from the surface of the Globe", V.I. Babkin3 demonstrates that 25% of the energy, flowing into the earth's surface is carried off by evaporation of water. That should be more than sufficient - the surface of the earth is 70% water and the solid soil is less capable of contributing to the evaporation - for such a lowering of the emissivity. Babkin's 25% is based on carefully collected data from the different oceans and solid surface regions at different geographical latitudes.
The two pictures below show the energy balance of the earth. Unfortunately not with equal axes. But the difference in fractions of the amount of outgoing energy - radiation and latent heat - is clear.
Figure 1
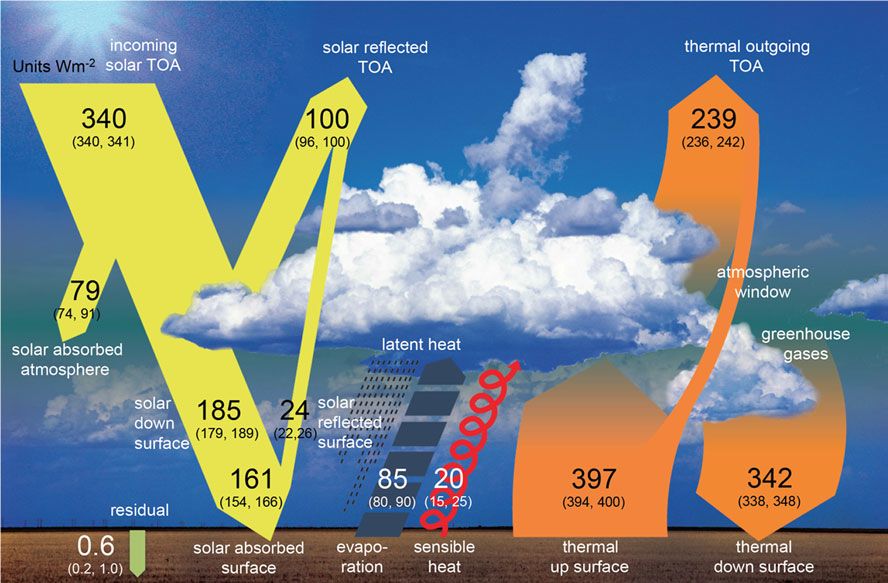
Figure 1. Existing (2018) model of the earth's energy currents; Wild e.o. 2013.
Figure 1, taken from a preprint of Rörsch4, shows the prevailing view on the radiation equilibrium, in which a large role is given to the return radiation from the atmosphere to the surface.
Figure 2.
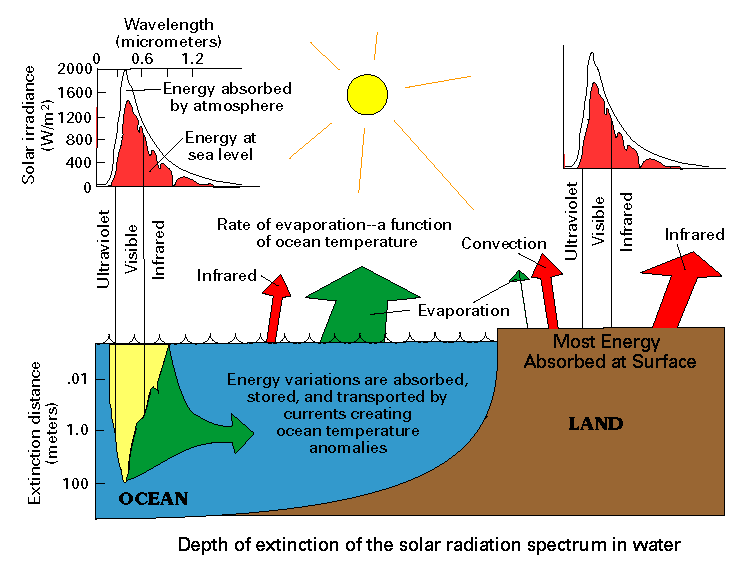
Figure 2. Eart's energy flows according to Geraint Hughes2 based on the work of Charles A. Perry.
Figure 2 shows the fraction of outgoing energy by means of latent heat mainly from the ocean, as a result of which the outgoing radiation decreases. It means that Figure 1 has to be changed on essential points. 'Convection' is missing from the picture at the surface of the ocean, but plays the same, though smaller, role as that of the evaporation. Both reduce the IR radiation.
In countless considerations, a temperature of 255 K acts as a starting point. And 'main stream' climatology explains the difference with the measured temperature, which is ~ 30 °C higher, by the atmospheric greenhouse effect. In my previous article, 255 K was the outcome for an ideal temperature-equalizing sphere. At unequal temperatures for a body such as the earth, the average is lower. The greenhouse therefore would have an even bigger gap to bridge. Hughes has shown that, in any case, part of that gap - if not all of it - is bridged by the heat accumulation of the oceans, which results in an emissivity reduction.
The results could be refined if the calculations were done rigorously using place and time-bound data of radiance in and out. Very often the mistake is made to equate average(T4) and (average(T))4.
Not only does the flux of the sun change with the geographical latitude and the time of the day. Also the albedo - of the sea in particular - changes and is location dependent. And with that, the amount of absorbed energy.
C. (Kees) le Pair
2018 11 01
Thanks to K. de Groot for
comments and language corrections
References
- C. le Pair: Kilimaat straling en temperatuur verevening-2; 2017 10 06.
- Geraint Hughes: The Watery Planet; 2018 08 21.
- V.I. Babkin: Evaporation from the surface of the Globe. HYDROLOGICAL CYCLE - Vol. II. © Encyclopedia of Life Support Systems (EOLSS).
State Hydrological Institute, St. Petersburg, Russia. - A. Rörsch: In search for autonomous regulatory processes in the global atmosphere; (Rethinking the model of the earth greenhouse). Ref. toegevoegd 2018 11 29.