
STRALING EN TEMPERATUURVEREVENING-2


door
C. (Kees) le Pair
Klimaatrealist
clepair@casema.nl
Samenvatting
Het klimaat verandert. Dat blijkt o.m. uit temperatuurmetingen. De Aarde inclusief atmosfeer is echter thermisch niet in evenwicht. Er vindt temperatuur verevening plaats o.a. door rotatie, door wind en door oceaanstromen. Die verevening beïnvloedt temperatuur gemiddelden. Dit opstel tracht een indruk te geven van de grootte van het effect door een berekening van het stralingsevenwicht van een lichaam (plaat, bol en bolschijven) tussen zon en heelal mèt en zonder die verevening. Een gemiddelde temperatuur kan door verevening ruim 100 °C hoger worden.
Inhoud
Om de leesbaarheid te vergroten zijn berekeningen en andere details weggelaten. Ze staan in de aanklikbare Appendix bij dit artikel.
- Inleiding
- Fysische parameters
zonneconstante
albedo
emissiviteit - Vlakke plaat
- Bol
- Bolschijven
- Discussie
- Dank
Noten
Appendix
1. Inleiding
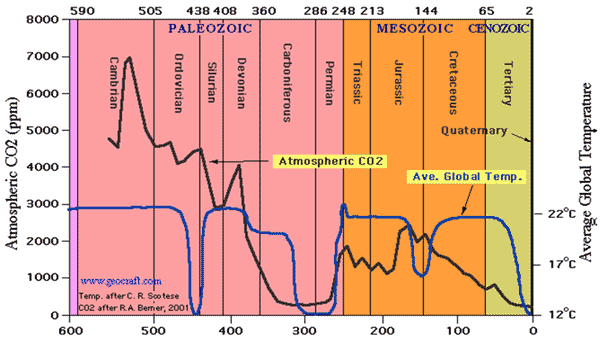
Het klimaat verandert zo lang de aarde bestaat. Onderstaande plaatjes laten dat zien. Het ene toont temperatuurverloop en dat van atmosferisch CO2 over 600 miljoen jaar, het tweede de atmosferische temperatuur over de laatste 400.000 jaar. In het grootste deel van de tijd waren er geen mensen die de verandering zouden hebben kunnen bewerkstelligen.
 |
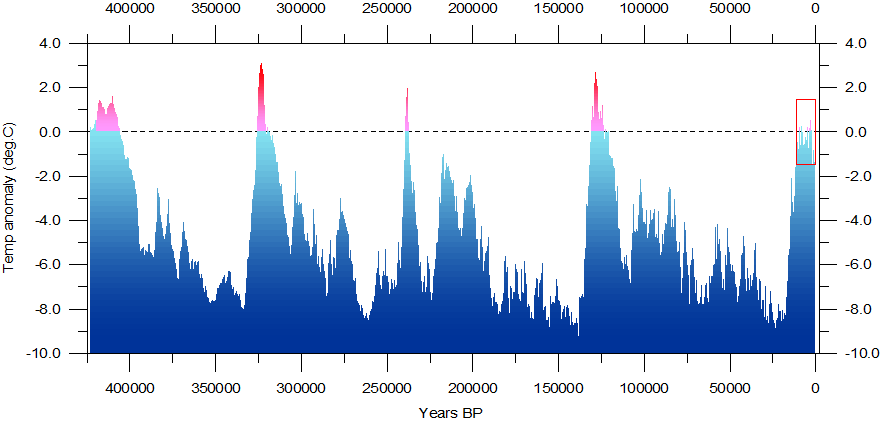 |
| Fig. 1. Temperatuur- en atmosferisch CO2 verloop laatste 600 miljoen jaar. | Fig. 2. Temperatuurverloop laatste 400.000 jaar, waarin de laatste vier ijstijden. |
Klimaatverandering was in het jaar 2015 aanleiding tot een conferentie van 196 wereldleiders in Parijs. Zij spraken af de verandering, die ze aan menselijk handelen toeschreven, tegen te gaan.
'Temperatuur van de Aarde' is geen eenduidig begrip. Het binnenste van de Aarde, de Kern, heeft een temperatuur van 5000+ K. (1 K = 1 °C, het nulpunt van de K-schaal is -273,15 °C). De aardmantel en de korst zijn kouder. 12 km hoog in de lucht vriest het 70 graden net als enkele keren per jaar in de buurt van de Noord- en Zuidpool. Op warme plaatsen op de grond kan het overdag 323 K (+50 °C) zijn. De gemiddelde temperatuur van de Aarde is daarom geen zinvol begrip. Meestal verstaan we er onder: de gemiddelde temperatuur van de onderste laag van de troposfeer gemeten op ~2 m hoogte berekend uit satelliet en ballon waarnemingen en thermometers die onregelmatig over het oppervlak zijn verdeeld. De opgegeven waarde is daar 288 K2). Dit is de gemiddelde temperatuur van een miniem stukje van de Aarde.
In tekst boeken (ref.1 & 2) en verhandelingen over klimaat vergelijkt men vaak de Aarde met een zwart stralende bol. Die ontvangt straling van de zon en van het heelal en stuurt om op een zelfde temperatuur te blijven evenveel straling terug in de ruimte. Door toepassing van de stralingswet van Stefan-Boltzmann (SB)
en uitgaand van gemeten inkomende straling en reflexibiliteit (gereflecteerde straling heeft geen invloed op de temperatuur) komt men tot een gemiddelde uitstralingstemperatuur en dito atmosferische temperatuur van 255 K.
In (1) is σ een constante met de waarde σ = 5,6703.10-8 Wm-2K-4 in vacuum7.
Het verschil tussen 255 K en 288 K wordt dan net als in de genoemde boeken toegeschreven aan broeikasgassen, die een deel van de straling absorberen.
Hierbij is de bijbehorende veronderstelling niet vermeld, dat die bol dan wel een uniforme temperatuur heeft. Of m.a.w. een ideale warmtegeleider is; beter nog: dat er volledige temperatuur verevening is. (Warmte wordt niet alleen door geleiding getransporteerd, ook door stroming en verder heeft rotatie een temperatuur vereveningseffect.)
Zonder die verevening verschilt de oppervlaktetemperatuur van een zwarte bol van plaats tot plaats. Het stralingsevenwicht geldt dan plaatselijk. De gemiddelde oppervlaktetemperatuur zou voor zo'n bol 154 K zijn (§4). Het verschil met de gemeten waarde van 288 K is niet 33° maar 134°. Verevening speelt dus een rol waaraan overigens Boeker e.a. (ref. 2) later (p. 44 e.v.) wel aandacht schenken.
De redenering is mank. Het is onjuist om een gemiddelde temperatuur van een miniem laagje te vergelijken met die van de Aarde als warmtestraler in zijn geheel.
In dit opstel licht ik de invloed van temperatuur verevening toe. Het is belangrijk, omdat bij gelijkblijvend verschil tussen berekende en gemeten waarden, verandering in de verevening een even grote maar tegengestelde verandering in de grootte van het 'broeikas effect' betekent.
In klimaatbeschouwingen wordt terecht geen rekening gehouden met de warmte afgifte van de aardkern en van de aardmantel. Die is zoveel kleiner dan de instroom van de zon, dat verwaarlozing gerechtvaardigd is, Appendix (A). Bovendien is het aannemelijk dat de aardwarmte niet verandert, terwijl dat voor andere parameters, zoals atmosferisch CO2 en de temperatuurverevening niet geldt.
2. Fysische parameters
De straling die de aarde met inbegrip van zijn atmosfeer van de zon ontvangt is niet alzijdig, maar gericht. De energieflux, ook wel de zonneconstante genoemd, is gemeten:
Iz = 1350 Wm-2(ref.1 p. 9) of 1370 (ref.2 p. 3). Wikipedia3 meldt gemiddeld 1360,8. Als gevolg van de elliptische baan om de zon is het maximum 1412 in januari en het minimum 1312 in juli. In dit opstel reken ik met:
De fractie α, het albedo, van de gereflecteerde zonnestraling, heeft geen invloed op de temperatuur. α is afhankelijk van materiaal, golflengte van het licht, invalshoek van de straling en structuur van het reflecterend oppervalk. Vanuit de ruimte gezien is het albedo van de aarde 37% à 39%4. In werkelijkheid is die van plaats tot plaats verschillend, zie fig. 3 en tabel 1.
|
Tabel 14 Albedo
Verse sneeuw of ijs : 80-95% Oude smeltende sneeuw : 40-70% Wolken : 40-90% Woestijnzand : 30-50% Grondaarde : 5-30% Toendra : 15-35% Grasland : 25-30% Bos : 10-20% Water : 10-60% De maan 7% (vulkanisch gesteente) Venus 72% |
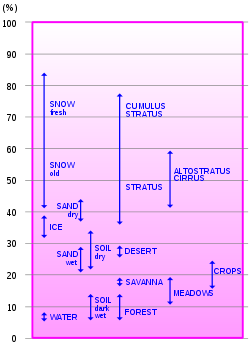
Fig. 3. Gemeten albedo waarden. |
De albedo verschillen en variaties maken een directe berekening van de op aarde plaatselijk ontvangen straling voor mij ondoenlijk. Daardoor verandert ook de zekerheid van de uitkomst van de plaatselijk berekende temperatuur. In dit opstel reken ik met verschillende waarden van α. In de genoemde tekstboeken en verhandelingen rekent men doorgaans met α = 0,3 voor de Aarde als geheel. De effectief inkomende zonnestraling wordt nu
Materie in een stralingsveld is geen zwarte straler. De emissiviteit ε is materiaal afhankelijk. Daarvoor is bij evenwicht op elke plaats de energieflux van de uitgaande straling Iu dankzij de stralingswet SB
Voor een zwarte straler is ε maximaal: ε = 1. Voor enkele andere materialen zie tabel 25. Ook ε is op aarde dus plaatsafhankelijk.
Tabel 25
| materiaal | ε |
|---|---|
| zuiver water | 0,96 |
| zout | 0,34 |
| sneeuw | 0,8 |
| asfalt | 0,88 |
| zand | 0,76 |
| cement | 0,54 |
| beton | 0,91 |
| ijzer roest | 0,61 |
| kalksteen | 0,92 |
In de derde plaats hebben we bij de aarde wat de straling betreft ook te maken met de materiaal afhankelijke transmissie. Materialen die de straling 100% doorlaten, warmen net als bij volledige reflectie niet op. Bij afnemende transmissie is er absorptie met als gevolg opwarming, die tevens afhangt van de warmtecapaciteit van het materiaal. Transmissie speelt een rol, bijvoorbeeld bij atmosfeer en water. Transmissie is golflengte afhankelijk. Indien I0 de inkomende straling is en I de straling na passeren van de materie, geldt voor de geabsorbeerde straling Ieff:
Waarin k de absorptieconstante van het materiaal bij die golflengte is. d is de dikte van het materiaal.
3. Vlakke plaat
Om het effect van temperatuurverevening op de gemiddelde temperatuur van een bestraald materiaal te berekenen beschouw ik eerst twee vlakke platen vrij in het heelal loodrecht op de inkomende zonnestraling even ver van de zon als de aarde in stralingsevenwicht. De ene plaat is een perfecte geleider, waarvan zon- en schaduwzijde altijd dezelfde temperatuur hebben. De andere is een ideale warmteïsolator. De zonzijde is in evenwicht met de inkomende zonnestraling, de achterzijde met die van het heelal, 3 K. Met het oog op paragrafen verderop kies ik voor het albedo, α = 0,3 en voor de emissiviteit, ε = 1.
De ideaal geleidende plaat straalt naar beide zijden evenveel uit, terwijl slechts één zijde de zonnestraling ontvangt. De 3 K straling vanuit het heelal is verwaarloosbaar.(4) & (2) wordt nu:
De gemiddelde temperatuur van een ideaal warmte geleidende plaat is dus:
Voor de isolator is het anders. De voorkant is in evenwicht met de inkomende zonnestraling, de achterkant met die van het heelal, d.w.z. Ta = 3 K. De temperatuur van de voorzijde, Tv, wordt bepaald door de zon. De straling bij 3 K verwaarloos ik. (4) & (2) wordt nu:
De gemiddelde temperatuur van een ideaal warmte geïsoleerde plaat is:
< T > = 182 K
Temperatuurverevening door warmtegeleiding verhoogt de gemiddelde temperatuur ten opzichte van de geïsoleerde plaat 120 °C.
Overigens is bij de isolator het verschil tussen de temperaturen van voor- en achterkant van de plaat: 364° (!).
4. Bol
Het geometrische verschil tussen plaat en bol heeft invloed op de gemiddelde temperaturen.
Ook hier onderscheiden we weer een ideaal warmtegeleidende bol en een zonder temperatuurverevening door geleiding, warmtestroming en rotatie. De straal van de bol is R.
In een bol met ideale warmtegeleiding is de temperatuur uniform en gelijk aan de gemiddelde temperatuur, maar wel afhankelijk van emissiviteit ε en albedo α. Met verwaarlozing van de 3 K heelal straling is de ontvangen stralingsenergie: flux x doorsnede van de bol (= πR2). De hele bol met oppervlak O = 4πR2 straalt energie uit met gelijke (= gemiddelde) temperatuur.
T = {0,25 Iz.(1 - α ) / σε}0,25 (6)
Het resultaat staat in tabel 3.
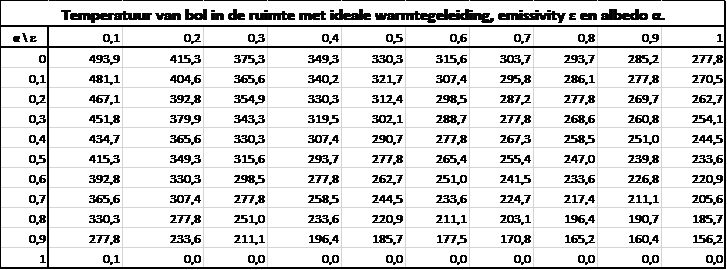
Bij α = 0,3 en ε = 1 komt het resultaat 254,1 K overeen met in de inleiding genoemde resultaat gemeld door anderen, 255 K. Die gingen derhalve uit van een bol met totale temperatuurverevening. De vergelijking met aardse omstandigheden gaat mank, omdat de temperatuur op aarde van plaats tot plaats verschilt.
We beschouwen ook een bol, waarin geen temperatuurverevening plaatsvindt.
Eén zijde is op de zon gericht. Eén punt ontvangt een flux van 1350 . (1 - α) Wm-2, de achterzijde heeft de heelal temperatuur 3 K. Aan de voorzijde varieert de flux met cos φ, waarin φ de hoek is tussen de richting waaruit de straling komt en die waar vanuit het centrum gezien het punt zich bevind. Een ring op het boloppervlak met breedte R.dφ en straal r = R.sin φ heeft dezelfde temperatuur, Tφ.
- R = straal van de bol
- r = straal van de cirkel op de bol
- Het oppervlak van een halve bol, c.q. van de koude zijde, Ok = 2πR2
- Het ringoppervlak, Oφ = 2πR2.sin φ.dφ
< Tφ > = {Iz.(1 - α) cos φ / σε}0,25
Op de achter helft van de bol is de temperatuur, Tk = 3 K.
De gemiddelde temperatuur van deze bol is nu per definitie:
gesommeerd, Appendix (B), over alle waarden van φ tussen 0 en π/2. De uitkomst voor verschillende waarden van α en ε staat in tabel 4.
Tabel 4
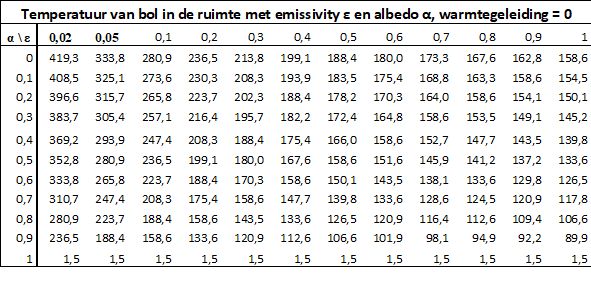
Bij een ideaal warmtetransport (temperatuurverevening) is bij α = 0,3 en ε = 1 de gemiddelde temperatuur ~ 110 °C hoger dan bij een bol zonder verevening.
De berekende gegevens van de twee verschillende bollen bij α = 0,3 als functie van ε zijn in fig. 4 in beeld gebracht, oneigenlijk samen met een horizontale lijn voor de gemeten gemiddelde temperatuur van het aardoppervlak (lage troposfeer, 288 K).
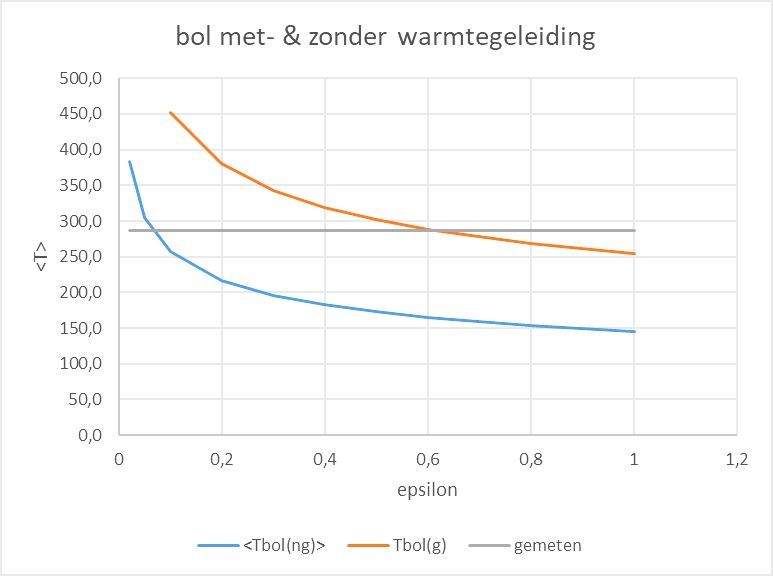
Fig. 4. ng = niet warmte geleidend, g = ideaal geleidend,
gemeten = gemiddelde aardoppervlak volgens de metingen.
5. Bolschijven
De Aarde transporteert warmte op allerlei manieren zoals door wind en oceaanstromen, verdamping enz. In Oost-West richting is er ook transport door de rotatie. Die is substantieel. Het maakt dat het 's nachts in plaats van 3 K niet veel kouder is dan overdag.
In deze paragraaf ga ik na hoe dat uitpakt voor schijven van een zwarte bol loodrecht op de rotatieas. Denk aan Aardse breedtegraden.
Beschouw een bol met straal R als boven, die roteert en die in zekere mate warmte vasthoudt. Rotatieas loodrecht op de inkomende zonnestraling.
Rotatietijd = θ (dus rotatiesnelheid ω = 2π/θ).
Flux van de zonenergie Ieff = (1 - α) I = 1000 Wm-2
Emissiviteit ε = 1
Albedo α = 0,3
Op de zongerichte 'meridiaan' is op een 'breedtegraad' φ de energie instroom per vierkante meter 1000.cos φ Wm-2.
De bol is verdeeld in schijven met dikte dy en straal r = Rcos φ.
y is parallel aan de rotatieas.
Zo'n schijf ontvangt per omwenteling aan zonne-energie:
Indien er geen warmtetraansport is over de bol in de y-richting, maar wel warmte-energie wordt vastgehouden, die in loop van een hele rotatie wordt uitgestraald, zodat de temperatuur op de bewuste plaats op de bol ten tijde θ weer gelijk is aan die bij t = 0, is er niet meer op elk moment en plaats stralingsevenwicht. We hebben dan op elk moment op elke plaats op de schijf een temperatuur T(t,φ) die via Stefan-Boltzman de daar uitgestraalde energie bepaalt.
De uitgestraalde energie per omwenteling is gelijk aan de ontvangen zonnestraling:
Gesommeerd over het het hele oppervlak A van de schijfrand met
ΔA = het uitstralend oppervlak op de schijf φ ten tijde t.
(7) en (8) geven de conditie voor de distributie van T(t,φ), Appendix (C):
De temperatuurdistributie over een schijf is afhankelijk van materiaaleigenschappen en daarom niet gedefinieerd. Die is voor water anders dan voor vaste stof. Twee gevallen, de extremen, zijn integreerbaar: volstrekte temperatuurverevening per schijf en de tegenpool: totaal geen verevening, dus instantaan plaatselijk temperatuur evenwicht tussen inkomende en uitgaande straling.
Volstrekte temperatuurverevening per schijf.
Indien rotatie van de bol met materiaal dat warmte opneemt, geleid en afgeeft snel genoeg is, waardoor de schijftemperatuur uniform zou worden gehouden, is T(t,φ) = T(φ). We hebben dan totale temperatuurverevening per schijf. T(φ) is dè temperatuur van schijf φ. Uit de conditie (9) volgt, Appendix (D), dan:
Het resultaat voor een zestal 'breedtegraden' is samengevat in onderstaande tabel:
| φ° | Tφ [K] |
|---|---|
| 0 | 274 |
| 20 | 269 |
| 40 | 256 |
| 60 | 230 |
| 80 | 177 |
| 90 | 0 |
Op de evenaarschijf is uitsluitend door totale temperatuurverevening 's nachts en overdag de temperatuur rond 1 °C (274 K).
Ter vergelijking middelen we deze temperaturen voor deze 6 breedtegraden elk met gewicht cosφ in verband met de verkorting van de breedtecirkels naar de pool toe. Op die manier gemiddeld SOM(T.cosφ) / SOM(cosφ) vinden we voor de temperatuur van de bol als gemiddelde ~257 K. Dat stemt overeen binnen de onnauwkeurigheden in de berekening met het gemiddelde gevonden voor soortgelijke hele bol: 254 K.
Totaal geen temperatuurverevening
Indien de vaste materie van de bol warmte niet zou vasthouden en geleiden moet voor evenwicht de energie-uitstraling overal steeds gelijk zijn aan de inkomende straling. De temperatuur aan de zijde die van de zon is afgewend is dus altijd 0 K.
Op een oppervlakje dAt,φ valt gedurende 0,5 θ per seconde in:
ψ is de hoek tussen de zonsrichting en de plaats van dAt,φ op de bolrand.
De daaraan gelijke uitstraling is:
De temperatuur op het punt (φ,t) is
We definiëren een gemiddelde temperatuur voor de ring:
Het resultaat van deze berekening, Appendix (E), is:
Voor een zestal 'breedtegraden' is de gemiddelde temperatuur van schijf φ samengevat in tabel 6:
| φ° | Tφ [K] |
|---|---|
| 0 | 156 |
| 20 | 154 |
| 40 | 146 |
| 60 | 131 |
| 80 | 101 |
| 90 | 0 |
De maximum temperatuur op deze bol zou bij 'breedtegraad' φ = 0 midden overdag 364 K zijn. Op die plaats zou het overigens de hele nacht 0 K zijn, net als aan de polen bij φ = ±90°.
Ter vergelijking middelen we deze temperaturen voor deze 6 breedtegraden elk met gewicht cosφ in verband met de verkorting van de breedtecirkels naar de pool toe. Op die manier gemiddeld {1/SOM(cosφ)} . SOM(Tcosφ) is de temperatuur voor de bol als gemiddelde ~147 K. Dat stemt binnen de onnauwkeurigheid van de berekeningen in met het gemiddelde gevonden voor de soortgelijke hele bol: 145 K.
6. Discussie
De uitkomsten van de berekeningen aan de hypothetische bol in de ruimte verschillen van die waarvan in de klimaatdiscussie sprake is. De Aardse omstandigheden zijn complex. Dit opstel diende slechts om te laten zien hoe groot het gevolg van temperatuurverevening is.
Het is onjuist om de gemiddelde temperatuur gemeten 2 m boven het Aardoppervlak, 288 K, de gemiddelde Aardtemperatuur te noemen. Het is de temperatuur van een schil, ongeveer de menselijke leefomgeving. Dat is een miniem deel van de Aarde inclusief atmosfeer, niet het hele lichaam dat in evenwicht is met de straling van zon en heelal. Indien dat wel het geval was, zou de Aarde bij 288 K afkoelen, want dan zou zij meer warmte verliezen dan ze van de zon ontvangt.
De Aardse temperatuur is niet uniform. Er zijn koude en warme onderdelen. De inkomende zonnestraling is plaats- en tijdsafhankelijk. Het albedo verschilt van plaats tot plaats en van tijd tot tijd net als de emissiviteit, ε. Ook is de Aarde in het stralingsevenwicht geen ondoorzichtig voorwerp. Het gedeelte dat aan de stralingswisselwerking deelneemt is deels transparant (atmosfeer en water). Dat deel absorbeert, transporteert en emitteert en beïnvloedt zo eveneens het evenwicht.
Het is een interessant climatologisch probleem te bepalen hoe het komt dat de menselijke leefomgeving een gebied is met de genoemde temperatuur. Dat probleem is nog niet opgelost.
In hoeverre het gerechtvaardigd is de 288 K de gemiddelde temperatuur van de onderste troposfeer te noemen is niet zeker. Thermometers zijn niet gelijkmatig over de wereld verdeeld. Ze zijn verplaatst, er zijn er toegevoegd en verwijderd. Satelliet-, ballon- en situ-metingen geven niet precies gelijke resultaten. Ik denk dat de term indicator temperatuur een betere naam zou zijn. Indien de thermometers en de satellietmeters, waarmee die berekend wordt, niet veranderen is de verandering van de indicator een onomstotelijk teken van klimaatverandering. Dat is ook het geval als veranderde meetomstandigheden bewijsbaar minder invloed hebben op de uitkomsten dan de gevonden veranderingen zelf.
De bolberekening toont dat de mate van temperatuurverevening door het warmtetransport van wind, oceaanstroming en rotatie de stralingsevenwichttemperatuur beïnvloedt. Dat betekent dat verandering in het warmte transport temperatuurverandering veroorzaakt; daarmee ook de temperatuur van afzonderlijke delen. We weten dat de oceaanstromen en de wind veranderlijk zijn. Hetzelfde geldt voor het albedo. Al of geen wolken bij de polen of bij de evenaar veranderen het albedo en de transmissie op verschillende manieren, ook tijdens de nacht.
Ik heb de indruk dat in veel klimaatbeschouwingen verondersteld is dat al deze effecten tezamen onveranderlijk zijn net als de zonnestraling. En alleen de samenstelling van de atmosfeer verandert. De concentratie van CO2 en andere gassen neemt toe. Dat verandert de emissiviteit en de transparantie en bijgevolg de temperatuur. Echter verwaarlozing van verandering in de andere factoren met name in de temperatuurverevening is onverantwoord.
NB. De hoeveelheid atmosferisch CO2 is slechts voor een klein deel het gevolg van menselijk toedoen. De oceaan bevat meer CO2 in opgeloste toestand en de evenwicht concentraties van water en lucht zijn afhankelijk van de temperatuur. Indien die bv. door verandering van de temperatuurverevening hoger wordt, waardoor de concentratie in de oceaan 1% zou afnemen, zou die in de atmosfeer ~ 50% stijgen. Maar CO2 is niet het onderwerp van dit opstel.
De Aarde verevent de temperatuur gedeeltelijk. Extremen als 0 K en 364 K komen aan het oppervlak niet voor. Maar tussen polen en sommige plaatsen in de tropen kan het verschil wel 100° zijn. Het verschil is kleiner dan op een niet geleidende zwarte bol. Er is warmtetransport. We mogen aannemen dat warmtetransport door geleiding tussen plaatsen verwaarloosbaar is. (Het binnenste van de aarde is > 5000 K. Indien de warmtegeleiding goed zou zijn, hadden we verbrande voeten.) Toch speelt geleiding een rol bij het plaatselijk opslaan van warmte die dankzij de rotatie dan weer op andere plaatsen ter beschikking komt. De voornaamste temperatuur-vereveningsmechanismen zijn:
- De rotatie van de aarde. (Verevening in Oost-West richting en via de Coriolis kracht ook op de stromingen.)
- Stroming van de oceanen.
- Stroming van de atmosfeer (Wind).
Totale verevening of helemaal niet heeft bij een effectieve ε = 1 >100° verschil in gemiddelde temperatuur tot gevolg en bij ε = 0,1 zelfs ~200°. Verandering van ε tussen 0,1 en 1 verandert bij totale verevening de gemiddelde temperatuur 112° en zonder verevening 200°.
Verevening verdient nader onderzoek. Die is veranderlijk en heeft een invloed op de temperatuur vergelijkbaar met veranderingen in albedo en emissiviteit, waaraan broeikasgassen als H2O, CO2, CH4 e.a. bijdragen.
6. Dank
Arthur Rörsch en Frans van den Beemt vestigden mijn aandacht op de rol die temperatuur verevening speelt in klimaat processen. (Hun publicatie, waarin zij o.a. een vergelijking maken met de atmosfeer- en oceaanloze maan, is in voorbereiding.)
Jo Hermans, o.a. auteur van het schitterende boek 'Energie survival gids'1, verschafte daarin enkele van de gebruikte gegevens en hielp met de oplossing van een essentiële berekening.
Vladimir Ponec corrigeerde een fout in mijn omschrijving van σ, zie ref. 7.
Nieuwegein, 2017 10 06.
Vervanging en uitbreiding
van een op 10 mei 2017
geplaatst artikel.
Commentaar
Zojuist ontving ik van Paul Braat het belangwekkende commentaar dat NASA in 1999 een bericht de wereld instuurde met 255 K als stralingsevenwicht temperatuur, waarop Nikolov en Zeller op soortgelijke manier als ik hierboven deed lieten zien dat het tussen de grenzen 154 K en 255 K is.
KRAMM, G. et. al. (2017). Using Earth's Moon as a Testbed for Quantifying the Effect of the Terrestrial Atmosphere Natural Science, 201pp: 251-288.
Voor het gemak volgt hier een verkorte samenvatting van Braat:
De 'gemiddelde' temperatuur van de naakte aarde zonder atmosfeer (Gray body), zou volgens NASA ongeveer 255 K zijn, krachtens de wet van Stefan-Bolzmann [NASA 1999]. De gemiddelde aardtemperatuur mèt atmosfeer meet ongeveer 288 K. Het verschil, het atmosferisch effect van de atmosfeer, zou in dat geval 288-255 = 33 K zijn. Maar volgens Nikolov en Zeller hield NASA geen rekening met de 'ongelijkheid van Hölder'; een rekenkundig gemiddelde van niet-lineaire functies produceert geen juiste gemiddelde waarde van afhankelijke variabelen... [Nikolov 2012]... Nikolov en Zeller berekenen op deze wijze de gemiddelde temperatuur van de naakte aarde op ~154 K. Als controle gebruiken zij de temperatuur van de maan. De temperatuur van de aarde zonder atmosfeer moet immers gelijk zijn aan de temperatuur van de maan, die op een zelfde afstand staat van de zon. NASA berekende de gemiddelde temperatuur van de maan op 255 K, maar sinds 2009 brengt een satelliet, het LRO Lunar Diviner Lunar Radiometer Experiment de temperatuur van de maan gedetailleerd in kaart [Diviner 2014]. De Diviner meet op de maan temperaturen van 390 K in de middag en ~95 K in de nacht, met een gemiddelde temperatuur van ~155 K; veel lager dan de 255 K van NASA en conform de berekening van Nikolov en Zeller voor de naakte aarde...
(Door Kramm e.a. later verbeterd. In het genoemde werk ontbreekt het effect van de aardrotatie op de verevening. En ik denk nog steeds dat de rol van verevening al ver voor 1999 onder fysici bekend moet zijn geweest. ClP).
6 nov. 2017,
- J. Hermans: Energie survival gids; BetaText 2008, p 76
- E. Boeker & R. v. Grondelle: Environmental Physics, p 4
- https://nl.wikipedia.org/wiki/Zonlicht (2017 05 07)
- https://nl.wikipedia.org/wiki/Albedo (2017 05 07)
- The engineering toolbox, http://www.engineeringtoolbox.com/emissivity-coefficients-d_447.html
- De oplossing dank ik eveneens aan Jo Hermans, RUL.
- Vladimir Ponec waarschuwde op 9/11/2017 dat σ afhankelijk is van de lichtsnelheid in het medium.